Numpy 傅立葉變換 np.fft (1)
一開始學傅立葉變換(Fourier Transform, FT)的時候,雖然懂得傅立葉的原理,但是感覺很不實在,因為無法碰觸到實際的操作,知道 FT 是從時間域到頻率域的轉換,但是不知道轉換後的結果是什麼樣子,因此我們就來看看 FT 的操作,印證所學的 FT 散落在各個角落沒有被提及的小特點,也許可以幫助更加熟悉 FT。
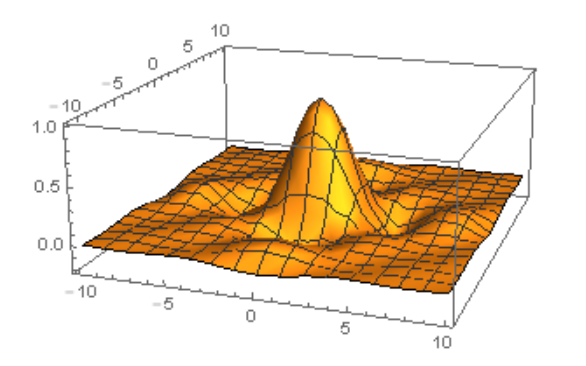
我們不看公式不看推導,但會印證結果。為了更加具象化,我們使用灰階圖像來操作,而不直接使用波。灰階圖像可以看是一組二維的陣列 a[x,y],在(x,y) 的座標裡面有 0-255 的數值,代表的是灰階圖像在 (x,y) 這個點上的亮度,0是最暗,255 是最亮。相像一下,如果 XY 是一個平面,而原本代表亮度的值是高低。如下圖。
所以,對圖像做 FT,也就是對信號(或說波形)做 FT。在做 FT 時,因為原始數據是離散的一個一個獨立數據(或稱信號採樣數據),所以稱為離散傅立葉變換(Discrete Fourier Transform, DFT) 。而我們使用的變換方式是計算速度比較快的FT ,稱為快速傅立葉變換(Fast Fourier Transform, FFT)。因此,在本篇文章的范圍內 FT 就是 DFT 就是 FFT。
首先,我們來看 lena 經過 FFT 之後,會變什麼樣子,先上代碼
import numpy as np
import matplotlib.pyplot as plt
import skimage.io as io
import src.genpic8 as pic
if __name__ == '__main__':
img = io.imread('asset/lena-gray.jpg')
fft = np.fft.fft2(img)
amp_spectrum_ns = np.log(np.abs(fft))
amp_spectrum_nl = np.abs(np.fft.fftshift(fft))
amp_spectrum = np.log(amp_spectrum_nl)
plt.subplot(221), plt.imshow(img, cmap='gray', vmin=0, vmax=255)
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(222), plt.imshow(amp_spectrum_ns, cmap='gray')
plt.title('non shift'), plt.xticks([]), plt.yticks([])
plt.subplot(223), plt.imshow(amp_spectrum_nl, cmap='gray')
plt.title('non log'), plt.xticks([]), plt.yticks([])
plt.subplot(224), plt.imshow(amp_spectrum, cmap='gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()
print('end')
首先讀入 lena_gray 然後放入 img 變數裡面做為原始圖像陣列。之後使用 np.fft.fft2 對原始圖像陣列做 FFT 然後存入 fft 變數裡面。這裡的 np.fft.fft2 是 Numpy 裡的 Fast Fourier Transform 子套件,fft2是二維傅立變換。
amp_spectrum_ns 變數存放的是低頻在四個角,還沒有使用 fftshift 移至中央,如下圖右上。
amp_spectrum_nl 變數存放的是沒有求自然數指數,數值類型為 float64 範圍很大 matplotlib 無法繪出,如下圖左下。
amp_spectrum 變數存放的是做完 FFT 之後的結果顯示,如下圖右下。
結論
我們在做完 FFT 之後,嚐試沒有做常規的處理 shift 及 log 並顯示結果。最後完成了熟悉的 FFT 結果圖。所以我們了解到,FFT完成後結果的低頻數據是存在四個角落,中間是高頻數據。為了顯示,我們才做 log 運算。
下一篇 我們將使用純白圖,上白下黑的圖片來做 FFT,並觀察其結果。