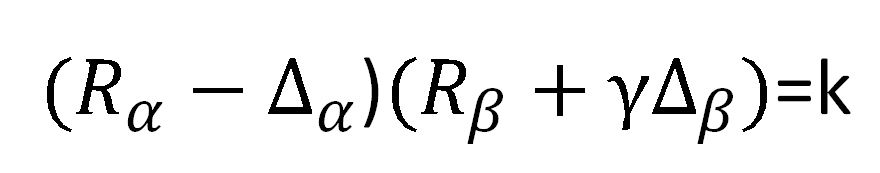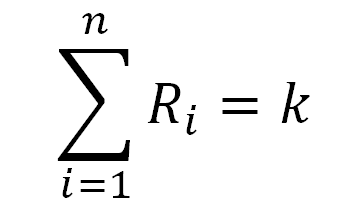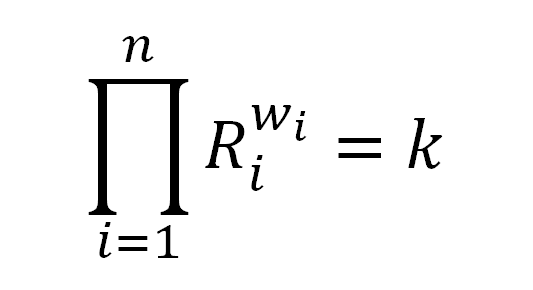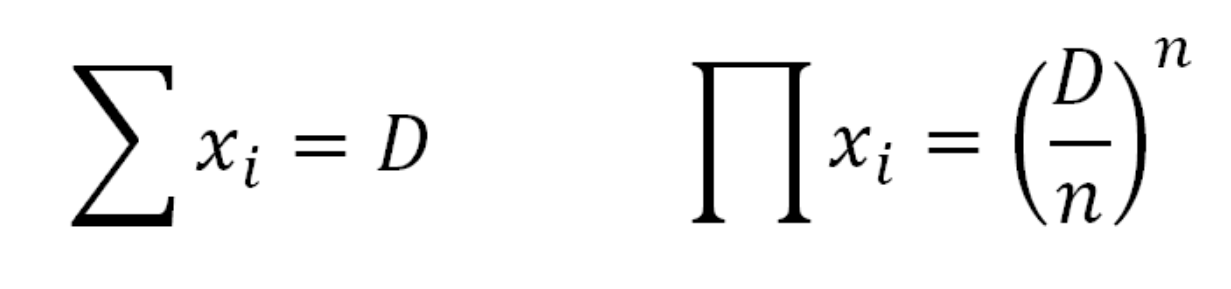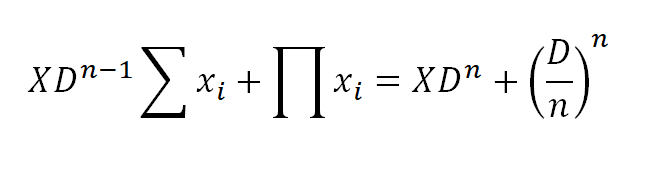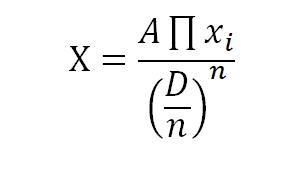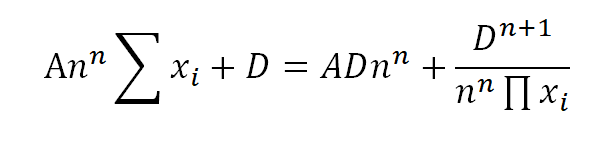StableSwap 公式之我見
自動做市商核心功能的其中一項,就是自動定價而不依賴鏈外或線下的報價。
自動定價之所以成為核心功能,是因為它要具備兩項功能,一獲利,二平衡資產價值。獲利就是交易雙邊的資產,其交易前總值應該等於或大於交易後總值。
這些可交易的資產稱為流動池,有的流動池只有兩種代幣,有的流動池有三種以上代幣,依照其交易理論公式的不同而定。
而我們今天要說明的是 Curve Finance 所使用的定價公式:StableSwap invariant,這是一種混合型恒定加總及恒定乘積公式 。
說明StableSwap使用的公式之前,會先簡介另外三個公式,恒定總和公式 Constant Sum Invariant,恒定乘積公式 Constant Product Invariant,恒定均值公式 Constant Mean Invariant。
恒定乘積公式 Constant Product
由 Uniswap 所率先使用也最有名。公式如下:
其中 R 代表資產的數量,α 及 β 代表資產種類,γ代表手續費,∆ 代表交易的資產,k 是一個恒定常數。
以上的公式,表示用戶使用 β 兌換出 α ,所以流動池裡的 α 資產是減少的,β資產是增加的。
而其中加入的 β資產是扣掉手續費γ之後的數量。忽略手續費時,這個公式也被簡化為 X*Y=K 。
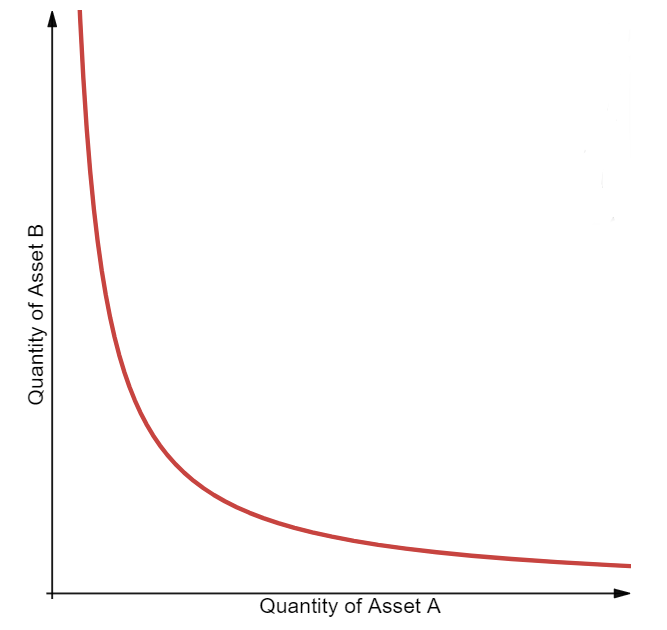
下圖代表在這個公式下的價格變代。
這張圖表示價格的變化,也就是資產的兌換數量關係。當資產A數量多的時候,可以兌換的資產B就減少,表示價格下降。當資產A數量少的時候,可以兌換的資產B增加,表示價格上昇。而最重要的是這個兌換曲線是一個雙曲線,這表示資產A或資產B在這個公式裡,數量不會是零,理想中提供了永遠可進行交易的可能性。
恒定總和公式 Constant Sum
這個公式是最簡單的,公式如下:
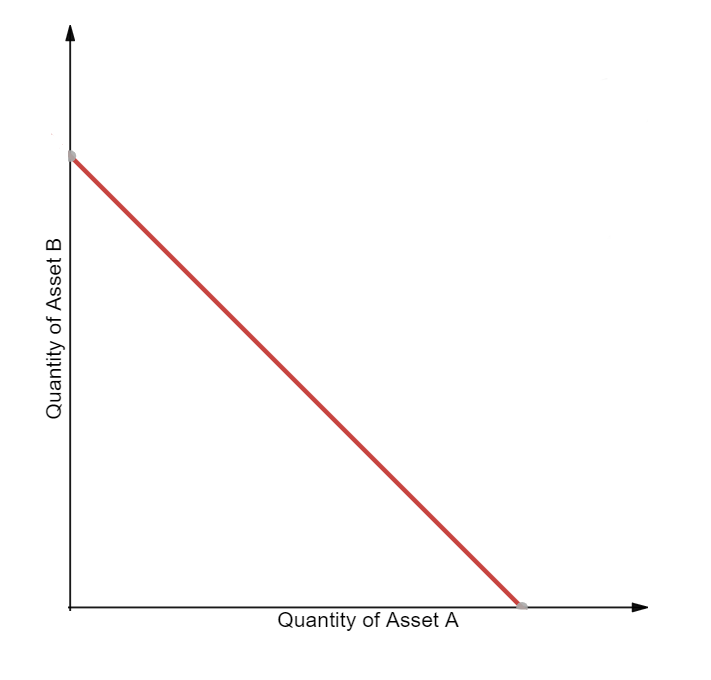
其中R是每種資產的數量, k 是常數。我們把價格變化繪制如下圖:
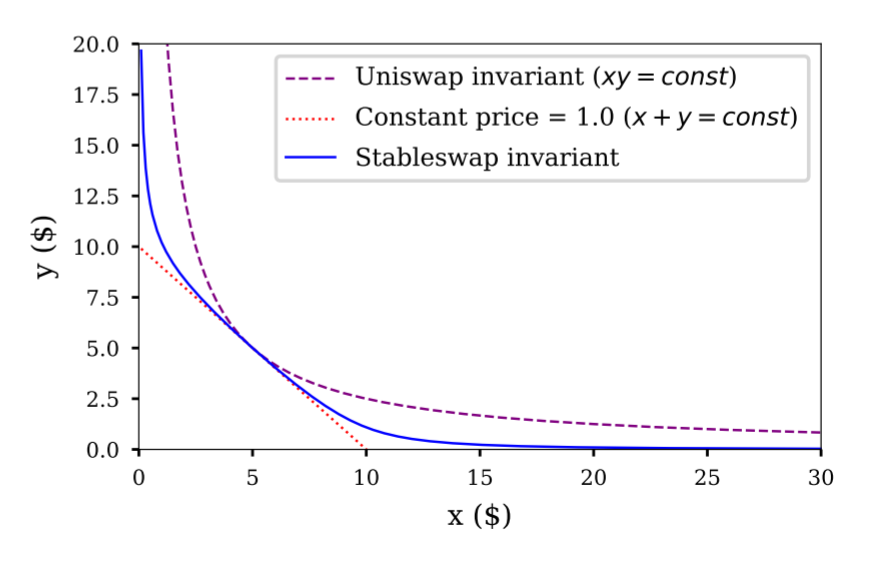
這個公式的特點是零滑點,意思就是說,交換多少的資產,就會在兌換價格中呈現而不失真。在其他的公式中,單次交易量越大,當次的價格失真越高;滑點越大,價格的失真度越高,代表產生的損失可能越大。
然後這個公式不會產生無限的流動池。意思就是說,資產A或資產B兌換後,數量是有可能為0的。看上一個恒定乘積公式,在理論上是提供無限的流量池,每個交易結束後都還有資產進行下一個交易。因此,這個公式並不適合做為自動做市的公式。
恒定均值公式 Constant Mean
這個公式是恒定乘積公式增加適用性而來的,這個公式允許2個以上的資產,並且加權不再是 50/50 。第一個使用的做市商是 Balancer ,在不計手續費的情況下滿足以下公式。
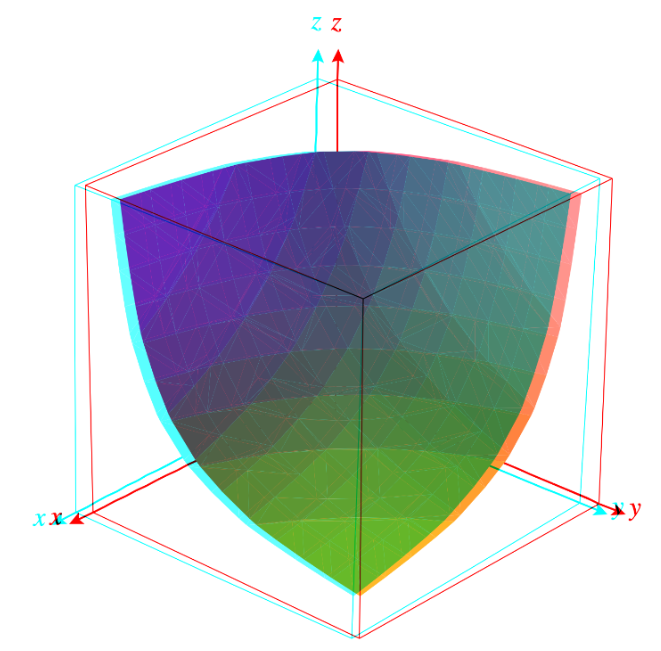
其中 R 是每種資產的數量,w是該資產的權重,k 是常數。這個公式,維持了資產加權平均數的恒定,如 Balancer 白皮書的封面所示,如下圖
各種資產依資產的權重恒定乘積。以上圖來說,如果三種資產等重,也就是各佔 1/3 的話,公式為 (x*y*z)^(1/3) = k
因為恒定均值做市可以允許多種資產,因此也有人稱這種方式為多維度自動做市商( N Dimentional Automated Market Maker) , Balancer 就是使用這種模式。
混合型恒定總合及恒定乘積公式 Hybrid Constant Sum and Constant Product (aka StableSwap from Cruve whitepaper)
StableSwap 的價格曲線特性是:在代幣平衡時較平坦像是恒定總加,代幣不平衡時就過渡為類似恒定乘積。如下圖中的藍色曲線。
我們來看看 StableSwap 是如何推導出這個公式的。
以下是恒定總和公式(下圖左)跟恒定乘積公式(下圖右)
其中 D 是所有代幣同等數量時,代幣的總和。
StableSwap 假設恒定總和要有無限槓桿,並且恒定總乘積有零滑點,並且具有放大的效果。因此用 X 來代表槓桿,乘上恒定總和公式,然後加進恒定乘積公式裡面。
此公式當 X 為 0 時, 是恒定總和,當 X 為無窮大時接近於恒定乘積,這樣的屬性是我們所需要的。其中 n 為代幣種類,應為無因次數(dimensionless)不為無窮大。
然後我們讓 X 動態,讓資產處於平衡時,能夠有一些流動性。
其中的A在資產達到平衡時會是一個常數,當資產越不平衡時則趨近於0。然後將 X 代入之前的公式裡面。
最終,StableSwap推導出這個混合型的公式。透過白皮書中對公推導的說明,我們了解這個公式想要達到的目的有兩個
1、資產趨近平衡時,也能有流動性
2、無論資產是否平衡,都能具備低滑點
白皮書中也給了針對三種代幣 DAI, USDC 及 USTD(應該是 USDT, 這裡可能是白皮書筆誤) 2019年5月-10月 的優化數據,
- 放大係數A 優化為 85
- 每次交易手續費 0.06%
- 流動利息312% APR
結論
不可諱言地,這個 Curve 導出的穩定幣專用的混合型恒定加總及恒定剩積公式非常的晦澀難懂,在導出的過程之中部份公式也引用也略過了。但是我們雖然沒有辦法透過推導公式去清楚了解含意,但是透過每一步的推導的說明,在假設公式正確的前提之下,最後的公式的確可以達到 Curve 所想要的兩個效果。
而我個對於這個公式的準確度,倒是抱著比較懷疑的態度,不是說這個公式錯了,而是我在想,當資產偏離平衡時,滑點必然出現,而且極端的情況下,一樣是會偏離實際價格很大,但我無法確定在這個極端的情況如何實現,但就是就如我在分析恒定乘積公式時所說的,在理論上提供無限的流動性。這裡,也是應該同樣的說明,在理論上還是會偏離實際價格。
具說另一個公式 shell protocol ,也是穩定幣公用的自動造市定價公式,不知道我有沒有機會一窺究竟呢?
圖片及資料來源:
https://www.curve.fi/stableswap-paper.pdf
https://medium.com/bollinger-investment-group/constant-function-market-makers-defis-zero-to-one-innovation-968f77022159